Escrito por Waldo Messias, estudante do Programa de Tutoria – Turma Avançada 2021
O relato da criação presente nos dois primeiros capítulos de Gênesis, descreve como Deus trouxe à existência cada aspecto da realidade, de modo que fizessem parte de um todo cujo resultado manifesta a glória de seu Criador. Foi do agrado de Deus que o homem e a mulher estivessem inseridos neste cenário, guardando e desfrutando (com restrição) daquilo que Deus havia criado.
É inevitável que cores e formas sejam notadas pela percepção humana. Sendo assim, os estudos acerca da geometria são empreendimentos teóricos que também nos possibilitam compreender o mundo em seus aspectos numérico e espacial. Contudo, como é possível teorizar acerca destas formas geométricas uma vez que experimentamos a realidade de forma integral? Como as geometrias se diferenciam umas das outras?
O filósofo calvinista holandês Herman Dooyeweerd (1894-1977), professor de direito e jurisprudência na Universidade Livre de Amsterdã, desenvolveu uma filosofia cristã, tomando como ponto de partida os pressupostos de uma cosmovisão bíblica[1]. Tal filosofia é importante para a compreensão acerca da origem do pensamento teórico em contraposição à pretensa autonomia do pensamento filosófico. A exposição das diferentes geometrias no presente artigo, nos auxiliará na compreensão da crítica do pensamento transcendental de Dooyeweerd.
A GEOMETRIA EUCLIDIANA
Euclides nasceu provavelmente por volta do ano 300 a.C, nos tempos áureos da cultura helenística, quando a Alexandria, no Egito, era conhecida como o centro do conhecimento daqueles dias. Ele foi professor de matemática na escola real de Alexandria e escreveu o livro “Elementos de Euclides”[2].
A geometria elementar, como é também conhecida, recebe esse nome devido a utilização do método axiomático em seu desenvolvimento, ou seja, as proposições que podem ser demonstradas por um processo lógico, são sustentadas por afirmações tomadas como verdade sem a necessidade de provas. Tomemos como exemplo o primeiro de quatro postulados[3] da Geometria Euclidiana: “Fique postulado traçar uma reta a partir de todo ponto até todo ponto”[4], ou seja, pode-se traçar uma única reta por dois pontos quaisquer. Esta noção é intuitiva e não carece de demonstração. Uma criança em idade escolar munida de um lápis e uma régua é capaz de compreender que dois “pontinhos” no caderno podem ser ligados por uma linha reta.
Em suma, a geometria elementar é o domínio no qual o método axiomático pode ser aplicado em situações que embora simples, resultam em conclusões altamente complexas[5].
GEOMETRIAS NÃO EUCLIDIANAS
As contribuições para o desenvolvimento do pensamento matemático a partir da geometria plana[6] são inestimáveis e sem precedentes, porém, é importante destacar que, embora muito conhecida por ser objeto de estudo do ensino básico nas escolas, não é a única a se dedicar a investigação acerca das formas. Os elementos de Euclides reúne em si conhecimentos das geometrias dedutivas e empíricas dos egípcios e babilônicos, respectivamente[7].
É importante destacar que sua aceitação não se deu de forma acrítica, muitos estudiosos se dedicaram a investigar a validade de suas proposições. Os quatro primeiros postulados se mostraram consistentes e foram amplamente aceitos, estudados e ensinados. O quinto, todavia, não foi bem “recebido” como postulado na sociedade matemática pois, não era de comum acordo que pudesse ser “facilmente presumido”[8] que, “por um ponto fora de uma reta m pode-se traçar uma única reta paralela a reta m”[9] (figura 1).
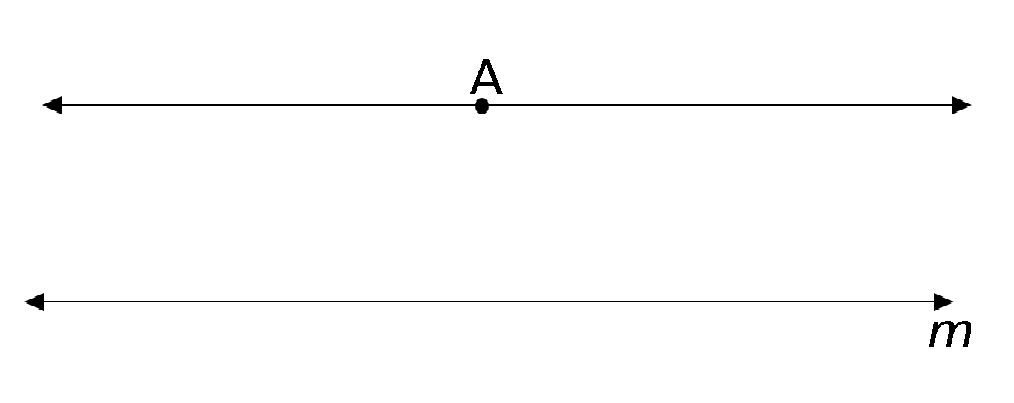
Figura 1
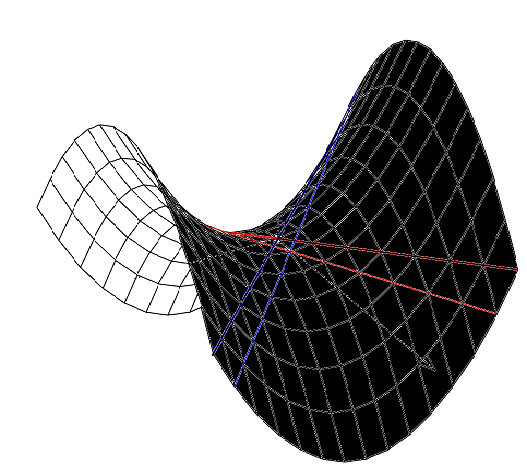
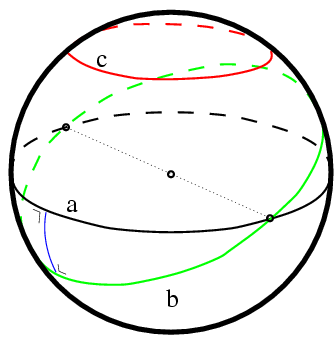
Foram elaboradas diversas tentativas de contraprovas, em que se afirmava que era possível sim haver mais de uma reta paralela passando por um ponto externo. Mas foi necessário cerca de 2000 anos para que dois jovens matemáticos – o russo Nicolai Ivanovich Lobachevsky e o húngaro Janos Bolyai – consolidassem as ideias e considerações em relação ao quinto postulado euclidiano[10]. As geometrias hiperbólica (figura 2) e elíptica (figura 3) são exemplos em que o “comportamento” das paralelas são diferentes em cada caso: no primeiro, existe mais de uma paralela passando por um ponto externo a uma reta; no segundo, não existem paralelas passando por um ponto externo a uma reta. Isso se dá devido às superfícies não planas, mas sim, curvas.
O final do século XVIII e início do século XIX, foi considerado por muitos historiadores o ápice das geometrias não euclidianas. Os estudos nessas áreas avançaram e Albert Einstein utilizou o espaço curvo na Teoria da Relatividade, mostrando que a nova geometria possui aplicação prática[11].
A “Geometria do Táxi” – considerada não euclidiana, embora não apresentasse nenhuma relação com o quinto postulado – foi um tipo diferente de geometria que “teve início na topologia com os estudos do russo Hermann Minkowski (1864-1909) o qual foi professor de Einstein”[12]. Visando uma aplicação prática e condizente com o dia-a-dia, a base para tal geometria se encontra na disposição das ruas representadas em uma malha retangular. Diferenças consideráveis podem ser constatadas em comparação à euclidiana, por exemplo, na representação de uma circunferência. O conceito de circunferência consiste em um conjunto de pontos que possuem uma mesma distância – conhecida como raio – de um ponto central:
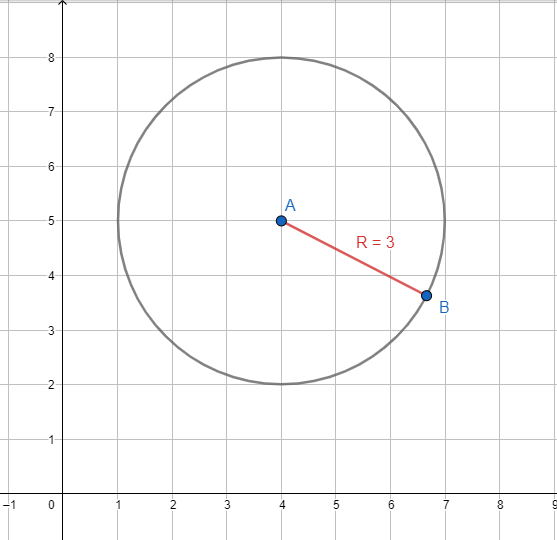
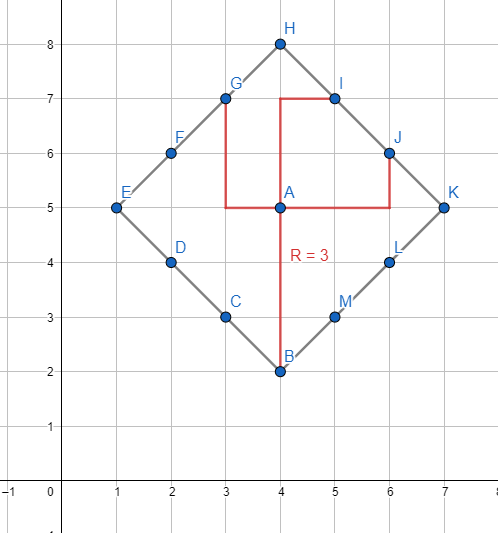
Em ambos os casos, o raio tem medida igual a três e os centros estão localizados sobre as coordenadas A(4,5). O que torna então a configuração de ambas tão distintas? Explicando de forma simples e sem considerar o rigor matemático, temos que: a primeira considera que a menor distância entre dois pontos é uma linha reta, podendo inclusive ser retas oblíquas[13]. Na segunda, a mesma distância é calculada considerando apenas deslocamentos verticais e horizontais.
Os axiomas que são aceitos ou recusados nas diferentes geometrias, nos permitem um vislumbre prático de que o pensamento teórico se apoia em suas pressuposições.
A CRÍTICA DO PENSAMENTO TRANSCENDENTAL
A história das geometrias exemplifica as implicações práticas dos pressupostos para um determinado sistema. Como vimos, para que uma circunferência assuma as características de um quadrado, basta que se assumam compromissos com uma outra configuração de plano. Contudo, o caráter axiomático não é exclusivo às ciências matemáticas, pois o mesmo acontece com qualquer atitude de pensamento.
Segundo Dooyeweerd, a autonomia do pensamento teórico foi elevada a uma condição intrínseca de verdadeira filosofia[14], permanecendo como a única das antigas certezas da filosofia que sobreviveu ao declínio causado pelo desenraizamento espiritual após as duas guerras mundiais[15]. É necessário, então, uma crítica radical ao dogma da autonomia, não apenas de um ponto de vista cristão, mas em qualquer tipo de reflexão filosófica verdadeiramente crítica[16].
O fato é que o pensamento filosófico que assume o dogma da autonomia não se sustenta, ou seja, não é um axioma consistente para a compreensão das relações fundamentais humanas. As filosofias grega, escolástica e secular moderna, por exemplo, partem desta mesma premissa mas chegam a conclusões fundamentalmente distintas[17]. As investigações acerca da geometria nos mostraram o contrário, ou seja, para que se alcance conclusões diferentes é necessário assumir axiomas diferentes. Dooyeweerd afirma:
“Se todas as correntes filosóficas que alegam estabelecer seu ponto de partida exclusivamente na razão teórica, de fato, não tivessem pressuposições mais profundas, seria possível resolver todas as discussões filosóficas entre elas de modo puramente teórico.”[18]
O dogma da autonomia não considera também a forma integral pela qual a realidade chega até o nosso horizonte temporal. A atitude teórica é uma antítese entre os aspectos não lógicos, frutos das experiências ordinárias, e os aspectos lógicos. Esta capacidade analítica permite uma abstração para que assim seja possível sintetizar conceitos que correspondam à realidade. Uma colméia de abelhas, por exemplo, não pode ser vista apenas como um aglomerado de hexágonos regulares, pois as propriedades geométricas são apenas um de seus aspectos modais[19]. Proceder desta forma, incorre-se em absolutização, a fonte de todos os ismos, em que um aspecto se sobrepõe aos outros[20]. Portanto, se os conceitos que representam a realidade são abstrações resultantes da antítese supracitada, não podemos tomar como dogma nenhuma formulação teórica, tampouco afirmar sua autonomia. Seria como provar a existência de triângulos utilizando como axioma a afirmação: “existem triângulos”.
Qual seria, então, o ponto de partida básico para o pensamento teórico que não esteja limitado ao horizonte temporal? É a “relação religiosa central entre o ego humano e Deus, a cuja imagem o homem foi criado”. Os compromissos que uma pessoa assume com seus pressupostos são de caráter supra teórico, ou seja, a síntese do pensamento não pode ser feita a partir da racionalidade. Sobre isso, Dooyeweerd afirma:
“O impulso religioso inato do ego em que sua relação com a Origem divina encontra expressão toma seu conteúdo de um motivo básico religioso como o poder espiritual central de nosso pensamento e ação.”[22]
Apenas com o discernimento deste impulso e suas implicações sobre o pensamento teórico é que se torna possível ter uma atitude crítica em relação ao pensamento filosófico. No momento em que o homem tomou como ponto de partida a autonomia da racionalidade, impossibilitou a existência de uma base comum para uma discussão filosófica. O que um dia prometeu iluminar, o lançou para mais longe do conhecimento da constituição básica da realidade e de seu Criador.
Acreditamos que o estudo teológico é fundamental para todo cristão, e não apenas para pastores ou líderes. Afinal, a teologia nos ajuda a seguir a Cristo em todos os aspectos da nossa vida!
No Loop, nossa equipe oferece suporte pedagógico e trilhas de estudo personalizadas para seus interesses, permitindo que você aprofunde seu conhecimento teológico e lide de forma segura com as situações do dia a dia.
[1] DOOYEWEERD, Herman. No Crepúsculo do Pensamento Ocidental: estudo sobre a pretensa autonomia do pensamento filosófico. Trad. Guilherme de Carvalho e Rodolfo Amorim de Souza. Brasília, DF: Editora Monergismo, 2018.
[2] Disponível em <https://www.ebiografia.com/euclides/#:~:text=Euclides%20foi%20um%20matem%C3%A1tico%20de,livro%20%22Elementos%20de%20Euclides%22.&text=Euclides%20de%20Alexandria%20nasceu%20provavelmente,centro%20do%20saber%20da%20%C3%A9poca>. Acesso em: 26 abr, 2021.
[3] O que se considera como fato aceito como verdade, sem a necessidade de demonstração; ponto de partida, implícito ou explícito, de uma argumentação; uma premissa.
[4] EUCLIDES, Os Elementos. Tradução e introdução de Irineu Bicudo. – São Paulo: Editora UNESP, 2009. 600 p.
[5] BARBOSA, J. L. M. Geometria Euclidiana Plana (com mais exercícios). 12. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2011. v. 1. 223 p.
[6] Geometria Euclidiana ou Elementar.
[7] GUSMÃO, N. L.; SAKAGUTI, F. Y.; PIRES, L. A. A geometria do táxi: uma proposta da geometria não euclidiana na educação básica <br> The táxicab geometry: a proposal non-euclidean geometry in basic education. Educação Matemática Pesquisa : Revista do Programa de Estudos Pós-Graduados em Educação Matemática, v. 19, n. 2, p. 213, 2017.
[8] Ibid., p. 213.
[9] BARBOSA, op. cit., p. 72.
[10] GUSMÃO, N. L.; SAKAGUTI, F. Y.; PIRES, L. A., op. cit., p. 216.
[11] Ibid., p. 216.
[12] Ibid., p. 216.
[13] Retas concorrentes que formam ângulos diferentes de 90°.
[14] DOOYEWEERD, op. cit., p. 42.
[15] Ibid., p. 41.
[16] Ibid., p. 42.
[17] Ibid., p. 43.
[18] Ibid., p. 44.
[19] Ibid., p. 48.
[20] Ibid., p. 62.
[21] Ibid., p. 72.
[22] Ibid., p. 75.
REFERÊNCIAS BIBLIOGRÁFICAS
BARBOSA, J. L. M. Geometria Euclidiana Plana (com mais exercícios). 12. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2011. v. 1. 223 p.
DOOYEWEERD, Herman. No crepúsculo do pensamento ocidental: estudo sobre a pretensa autonomia do pensamento filosófico. Tradução Guilherme de Carvalho e Rodolfo Amorim de Souza – Brasília, DF: Editora Monergismo, 2018.
EUCLIDES. Os Elementos. Tradução e introdução de Irineu Bicudo. – São Paulo: Editora UNESP, 2009. 600 p.
FRAZÃO, Dilva. Euclides. O Matemático de Alexandria. Ebiografia, 2021. Disponível em <https://www.ebiografia.com/euclides/#:~:text=Euclides%20foi%20um%20matem%C3%A1tico%20de,livro%20%22Elementos%20de%20Euclides%22.&text=Euclides%20de%20Alexandria%20nasceu%20provavelmente,centro%20do%20saber%20da%20%C3%A9poca>. Acesso em: 26/04/2021.
GUSMÃO, N. L.; SAKAGUTI, F. Y.; PIRES, L. A. A geometria do táxi: uma proposta da geometria não euclidiana na educação básica <br> The táxicab geometry: a proposal non-euclidean geometry in basic education. Educação Matemática Pesquisa : Revista do Programa de Estudos Pós-Graduados em Educação Matemática, v. 19, n. 2, p. 211-235, 2017.
